Page 16 - ATA YAYINCILIK 8. Sınıf Matematik Yazılı Soruları

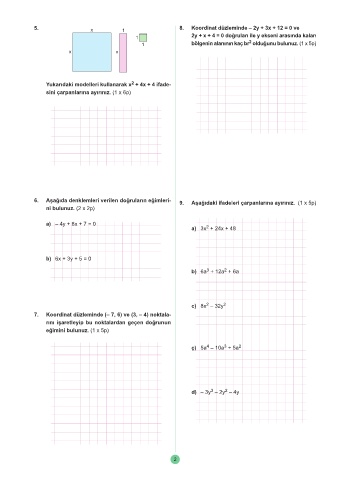
5. x 1 8. Koordinat düzleminde – 2y + 3x + 12 = 0 ve
1 2y + x + 4 = 0 doğruları ile y ekseni arasında kalan
2
1 bölgenin alanının kaç br olduğunu bulunuz. (1 x 5p)
x x

2
Yukarıdaki modelleri kullanarak x + 4x + 4 ifade-
sini çarpanlarına ayırınız. (1 x 6p)

6. Aşağıda denklemleri verilen doğruların eğimleri- 9. Aşağıdaki ifadeleri çarpanlarına ayırınız. (1 x 5p)
ni bulunuz. (2 x 2p)

a) – 4y + 8x + 7 = 0
2
a) 3x + 24x + 48

b) 6x + 3y + 5 = 0
3
2
b) 6a + 12a + 6a

2
c) 8x – 32y 2
7. Koordinat düzleminde (– 7, 6) ve (3, – 4) noktala-
rını işaretleyip bu noktalardan geçen doğrunun
eğimini bulunuz. (1 x 5p)

3
4
ç) 5a – 10a + 5a 2

2
3
d) – 3y – 2y – 4y

2 2